Diese Seite funktioniert nur mit Javascript.
Die Produktions-Box5.1.2.1 Die TransformationskurveMathematische Herleitung der Transformationskurve
s wird Sie kaum überraschen, dass es im Produktionsbereich auch noch eine Parallele zur Nutzenmöglichkeitskurve im Konsumbereich gibt. Um sie aufzuzeigen, wird in Abbildung 1 ein "Bier-Zigaretten-Güterraum" aufgespannt, in den von der Effizienzkurve die an den Isoquanten ablesbaren Produktionsmengen Punkt für Punkt übertragen werden. Das Ergebnis heißt Transformationskurve. Die Achsenabschnitte der Transformationskurve entsprechen den beiden Ursprüngen der Produktions-Box.
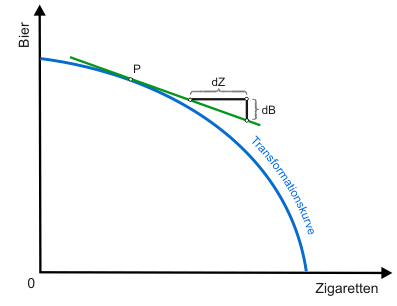
und wird daher oftmals auch so bezeichnet.
Jedoch sind natürlich auch alle Punkte unter ihr realisierbar, indem entweder Faktoren nicht vollbeschäftigt sind oder die Grenzraten der technischen Substitution in den verschiedenen Verwendungen nicht übereinstimmen. Ein Punkt unterhalb der Transformationskurve korrespondiert also mit einer Produktionsbox, bei der wenigstens eine Kantenlänge kleiner ist als die Faktorausstattung oder mit einem Punkt in der Box, der nicht auf der Effizienzkurve liegt.
Ihr kommt eine wichtige Bedeutung zu. Sie zeigt an, wie viel Einheiten eines Gutes eine Volkswirtschaft aufgeben muss, wenn von dem anderen Gut eine zusätzliche Einheit hergestellt werden soll. Sie zeigt also jeweils die Opportunitätskosten (synonym: Alternativkosten oder Verzichtskosten) der Produktion in Einheiten des anderen Gutes an.
Der in Abbildung 1 skizzierte konkave Verlauf ist für Transformationskurven typisch. Zwei verschiedene Ursachen können allein oder zusammen dafür verantwortlich sein. Eine Ursache sind
- unterschiedliche Kapitalintensitäten in der Produktion der beiden Güter,
die andere mögliche Ursache
Eine der beiden Ursachen ist für einen konkaven Verlauf immer notwendig, jedoch ist nur die unterlinear-homogene Produktionsfunktionen, wenn sie für beide Güter zutrifft, hinreichend. Der Effekt unterschiedlicher Kapitalintensitäten kann durch überlinear-homogene Produktionsfunktionen in Richtung auf ganz oder teilweise konvex verlaufende Transformationskurven überkompensiert werden.
Bevor wir die beiden Gründe mit Hilfe einer grafischen Darstellung in Abbildung 2 illustrieren, wollen wir zunächst Plausibilitätsüberlegungen anstellen. Für den Fall unterlinear-homogener Produktionsfunktionen ist dies nicht weiter schwierig. Ein Homogenitätsgrad von bspw. r = 0,5 bedeutet ja, dass eine Verdoppelung der Produktionsmenge erst mit einer Vervierfachung des Faktoreinsatzes erreicht wird. Eine Skalenelastizität kleiner eins bewirkt, dass zunehmende Produktionssteigerungen bei einem Gut je produzierter Einheit immer mehr Faktoren binden. Umgekehrt heißt das, dass relativ kleine Produktionsmengen mit relativ geringem Faktoreinsatz je Einheit realisierbar sind. Wir wollen nun annehmen, für Bier gelte eine unterlinear-homogene und für Zigaretten eine linear-homogene Produktionsfunktion. Um die Überlegung so einfach wie möglich zu gestalten, gehen wir von einem notwendigen Faktoreinsatz von einer Einheit Arbeit und einer Einheit Kapital je herzustellender Zigaretteneinheit aus. In Kapital und Arbeit ausgedrückt ist damit der "Zigarettenpreis" für jede denkbare Produktionsmenge konstant (wenn man bereit ist, diese Faktorbindung als "Preis" zu akzeptieren). Anders sieht es aber aus, wenn für die Zigaretten die Opportunitätskosten in Biereinheiten betrachtet werden. Nehmen wir dazu an, wir befänden uns auf der Transformationskurve in einem Punkt, wo die Grenzrate der Transformation Alternativkosten der Zigaretten in Höhe von zwei Biereinheiten anzeigt: Der Preis für Z beträgt im Moment 2B. Bewegen wir uns nun auf der Transformationskurve in Richtung mehr Bier und weniger Zigaretten, dann steigt annahmegemäß der durchschnittliche Faktoreinsatz beim Bier, während er bei Zigaretten mit je einer Faktoreinheit konstant bleibt. Also sinkt der "Zigarettenpreis" gemessen in Biereinheiten: Der Preis für Z beträgt jetzt weniger als 2B, weil für die Herstellung von zwei Einheiten Bier mehr Ressourcen benötigt werden als für die Herstellung einer Einheit Zigaretten. Wird die Bierproduktion auf Kosten der Zigarettenproduktion weiter ausgedehnt, so müssen die Alternativkosten der Zigaretten weiter abnehmen. Da die Alternativkosten jedoch gerade der Grenzrate der Transformation entsprechen, nimmt die Steigung der Transformationskurve kontinuierlich ab, wenn wir uns aus dem vorgegebenen Ausgangspunkt in Richtung Zigaretten bewegen und umgekehrt. Unterlineare Homogenität der Produktionsfunktionen für beide Güter verstärkt diesen Konkavitätseffekt. Die Konkavität der Transformationskurve spiegelt also in gewisser Weise wider, dass Produktionsausweitungen für Güter mit einer Skalenelastizität kleiner Eins zunehmend mehr Ressourcen binden.
Der zweite Grund für Konkavität ist (noch) schwieriger einzusehen und wir wollen es daher in diesem Absatz ausnahmsweise mal nicht so ganz genau nehmen und uns wirklich auf eine Plausibilitätsebene herablassen. Dazu nehmen wir an, Zigaretten werden relativ kapitalintensiv hergestellt, weil Kapital hier ein "produktiverer" Faktor als beim Bier ist. Demzufolge wird Bier relativ arbeitsintensiv hergestellt, da die gesamtwirtschaftliche Kapitalintensität ja durch die fix vorgegebenen Faktormengen konstant ist. Grafisch bedeutet dies, dass die Effizienzkurve in der Produktionsbox ständig oberhalb der Diagonalen verläuft. Würden nur Zigaretten und kein Bier hergestellt, dann müsste zwangsläufig die Kapitalintensität in der Zigarettenproduktion mit der gesamtwirtschaftlichen Kapitalintensität übereinstimmen. Analog lässt sich der Gedanke für die Bierproduktion nachvollziehen. Sowohl für die arbeitsintensive Bier- als auch für die kapitalintensive Zigarettenproduktion würde diese vollständige Spezialisierung keinen günstigen "Faktormix" bedeuten, d. h. ein Faktor wäre sehr reichlich vorhanden, der andere sehr knapp. Die Situation verbessert sich relativ, wenn beide Güter produziert werden. Dann kann nämlich in die Zigarettenproduktion relativ "viel" vom hier vergleichsweise knappen Kapital und in die Bierproduktion relativ "viel" von der dort vergleichsweise knappen Arbeit gelenkt werden. Bei beiden Gütern verbessert sich im Vergleich zur vollständigen Spezialisierung der "Faktormix". Beide Güter werden demzufolge gemessen in Einheiten der anderen relativ günstig produziert, während sich mit zunehmender Spezialisierung in der einen oder anderen Richtung diese Alternativkosten kontinuierlich erhöhen würden, was einer Konkavität der Transformationskurve gleichkommt.
Um die Transformationskurve grafisch herzuleiten, ist es notwendig, an den Begriff der Niveauproduktionsfunktion zu erinnern. Sie zeigt für homogene Produktionsfunktionen den Output in Abhängigkeit eines Faktors bei konstanter Kapitalintensität (s. Kasten). Sie ist damit eine Produktionsfunktion bei totaler Faktorvariation, da sich bei konstanter Kapitalintensität der Einsatz des Faktors Kapital ebenso vervielfacht wie der Einsatz der Arbeit oder umgekehrt - je nachdem, welcher der beiden Faktoren für die Darstellung gewählt wird.
In Abbildung 2 wird im II. Quadranten eine Produktions-Box für Bier und Zigaretten gezeigt. Es wird angenommen, dass beide erörterten Gründe für die Konkavität der Transformationskurve vorliegen; Zigaretten seien weiterhin das relativ kapitalintensive Gut.
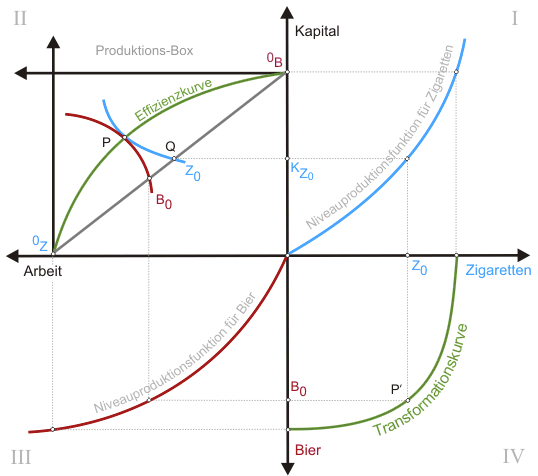
Die Diagonale in der Produktions-Box wird als Hilfsgerade benötigt, um über die Niveauproduktionsfunktionen im I. und III. Quadranten die Produktionsmengen im IV. Quadranten als Transformationskurve abtragen zu können. In der Steigung der Diagonalen kommt die gesamtwirtschaftliche Kapitalintensität zum Ausdruck, da die Länge der Box die Arbeits- und die Höhe die Kapitalausstattung der Wirtschaft anzeigt. Für diese Kapitalintensität ist im I. Quadranten eine Niveauproduktionsfunktion für Zigaretten in Abhängigkeit vom Kapitaleinsatz eingezeichnet; im III. Quadranten wird dementsprechend eine Niveauproduktionsfunktion für Bier in Abhängigkeit vom Arbeitseinsatz konstruiert.
Um das Gegenstück P' im IV. Quadranten zum Punkt P im II. zu finden, betrachten wir als Beispiel die Isoquante Z0 für Zigaretten. Da auf einer Isoquante die produzierte Menge in jedem Punkt konstant ist, können wir zum Punkt Q übergehen, ohne die Zigarettenmenge zu verändern. Um die Menge tatsächlich im Punkt Q zu erzeugen, wird bei der gesamtwirtschaftlich vorgegebenen Kapitalintensität der Kapitaleinsatz KZ0 benötigt. Für eben diese Kapitalintensität haben wir aber im I. Quadranten die Niveauproduktionsfunktion konstruiert, so dass wir jetzt die der Isoquante Z0 zugehörige Zigarettenmenge auf die Abszisse des I. Quadranten abbilden können.
Vollkommen analog - nur jetzt gegen den Uhrzeigersinn - lässt sich die Aktion für Bier wiederholen. Damit ist der Punkt P', der auf der Transformationskurve liegen muss, gefunden. Um die gesamte Transformationskurve vollständig abbilden zu können, muss die Aktion lediglich für ausreichend viele Punkte auf der Effizienzkurve wiederholt werden.